Goal First Optimization
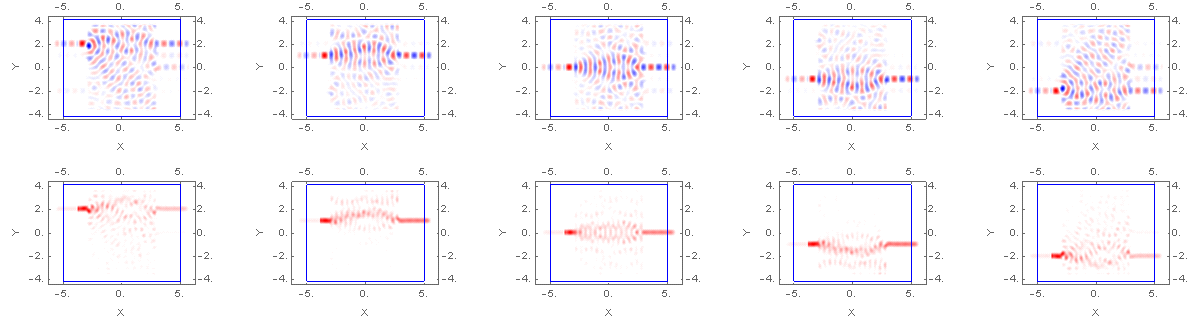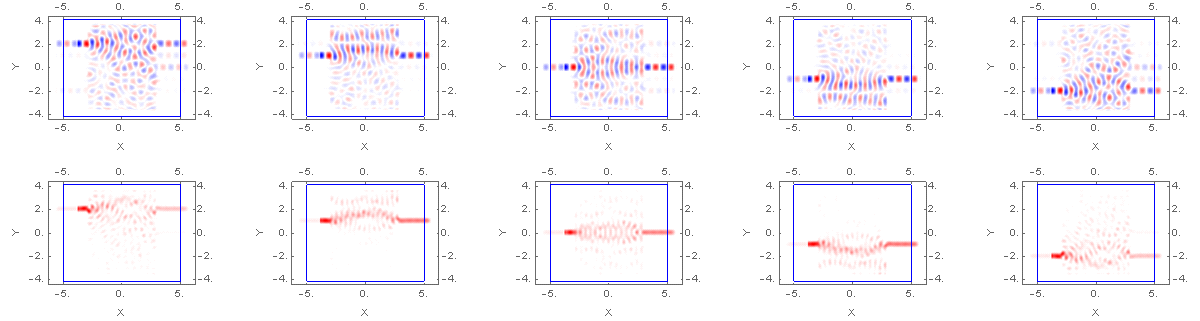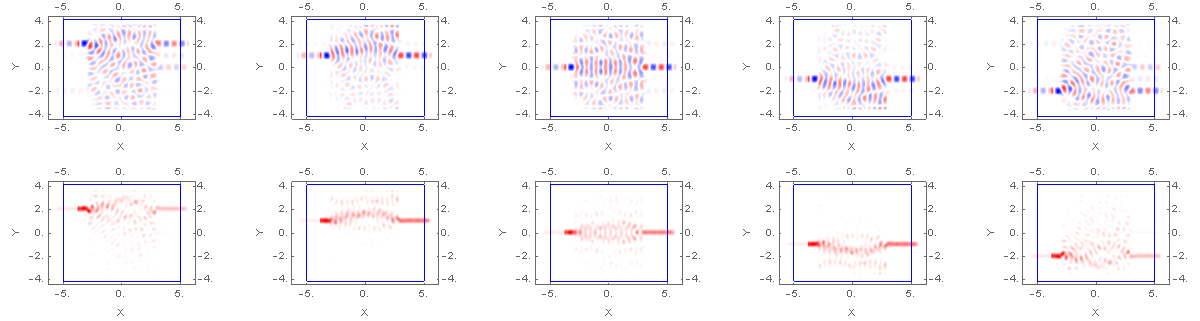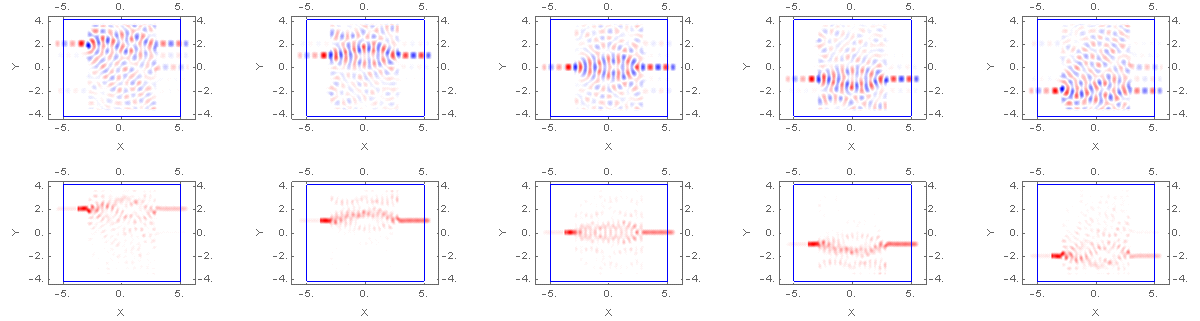
Fig 1. Optimization evolution of five goal functions. Namely, we want the system to converge such that the waveguides map directly across the structure. Permittivity is on the left (white = 0, black = 2) The phase snapshots are in the top row (blue = -1, white = 0, red = +1). The electric energy density plot is in the bottom row (white = 0, red = 1).
Fig 2. Resulting permittivity profile at the conclusion of the optimization.
This is most definitely not my invention. I merely implemented my interpretation of the work of Jelena Vuckovic and her students. I found it incredibly fascinating and a fundamentally different design paradigm from what I had seen in the half-dozen solvers I've used over the years.
In contrast, frequency-domain (FD) techniques, look at the scene from the point of view of a single frequency. Using the frequency domain version of Maxwell's Equations, we can mathematically express how each point in space interacts with the other. This creates a system of constraints which, if formulated correctly, will be equal in size to the number of unknowns in the system. In other words, the system is determined and square. Solving this problem reduces to inverting this system.
However, this technique opens up an interesting opportunity. What if the formulation of the problem contained more constraints than unknowns? For instance, one could include constraints on various ports in the system that not only expressed how much energy came in, but also how much energy was leaving. This is never done in commercial software because there is no physical way to create a port which "sucks" energy out of the system. It will create systems which (while desired) are impossible, and any solution would be fundamentally flawed. The system will now be over-determined and rectangular. However, while unphysical, the resulting solution from this minimization problem would be the fields that are nearest to being physical that satisfies these constraints. Since we are prioritizing satisfying the goal over the physics, Vuckovic and her team refers to this as "goal-first." Is this field useful?
What is interesting about these fields is that they provide a suggestion for how to change the structure. Given that we know both the electric and magnetic fields, we can solve Maxwell's equations for permittivity to yield
$$\mathbf{\epsilon} = \nabla \times \mathbf{H}/(j \omega \mathbf{E})$$
This formula can be applied to these unphysical fields from multiple desired port constraints to yield several permittivity suggestions. These suggestions can be averaged and used to calculate a "permittivity step direction" which is used to calculate a new permittivity. Various filters can be applied to this process in an attempt to coax out manufacturable structures. From here, the process simply repeats. With each iteration, the residue decreases until unphysical fields are actually not very unphysical at all.
I wrote my own Finite Difference Frequency Domain (FDFD) code in Mathematica, complete with PMLs. Several tweaks need to be made to consider the rows of the system matrix as constraints to be minimized. For instance, they should all share a common unit. Additionally, the source terms are now constraints and represent new rows in the system. Finally, one must find a quick Least-Squares Minimization solver. I found Matlab's to be better for this purpose than Mathematica's. My code sends the matrices to a Matlab server to be solved and then returns the result for further processing and filtering.
As a test case, I considered a multiplexor interfacing ten waveguides. The goal (albeit trivial) is to transfer the energy directly across the system so that the top waveguide on the left transfers its energy to the top waveguide on the right. Fig 1 above shows how the permittivity evolves through the optimization process. You can see that with each iteration the energy becomes more tightly confined to the target waveguide. Fig 2 shows the resulting permittivity. Finally, Fig3 below, shows the final field profiles.
Fig 3. The resulting fields at the conclusion of the optimization.